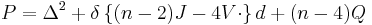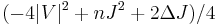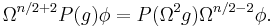Paneitz operator
In the mathematical field of differential geometry, the Paneitz operator is a fourth-order differential operator defined on a Riemannian manifold of dimension n. It is named after Stephen Paneitz, who discovered it in 1983, and whose preprint was later published posthumously in Paneitz 2008. It is given by the formula
where Δ is the Laplace–Beltrami operator, d is the exterior derivative, δ is its formal adjoint, V is the Schouten tensor, J is the trace of the Schouten tensor, and the dot denotes tensor contraction on either index. Here Q is the scalar invariant
which in four dimensions yields the Q-curvature.
The operator is especially important in conformal geometry, because in a suitable sense it depends only on the conformal structure. Another operator of this kind is the conformal Laplacian. But, whereas the conformal Laplacian is second-order, with leading symbol a multiple of the Laplace–Beltrami operator, the Paneitz operator is fourth-order, with leading symbol the square of the Laplace–Beltrami operator. The Paneitz operator is conformally invariant in the sense that it sends conformal densities of weight 2 − n/2 to conformal densities of weight −2 − n/2. Concretely, using the canonical trivialization of the density bundles in the presence of a metric, the Paneitz operator P can be represented in terms of a representative the Riemannian metric g as an ordinary operator on functions that transforms according under a conformal change g ↦ Ω2g according to the rule
The operator was originally derived by working out specifically the lower-order correction terms in order to ensure conformal invariance. Subsequent investigations have situated the Paneitz operator into a hierarchy of analogous conformally invariant operators on densities: the GJMS operators.
The Paneitz operator has been most thoroughly studied in dimension four where it appears naturally in connection with extremal problems for the functional determinant of the Laplacian (via the Polyakov formula; see Branson & Ørsted 1991). In dimension four only, the Paneitz operator is the "critical" GJMS operator, meaning that there is a residual scalar piece (the Q curvature) that can only be recovered by asymptotic analysis. The Paneitz operator appears in extremal problems for the Moser–Trudinger inequality in dimension four as well (Chang 1999)
See also
References
- Branson, Thomas P.; Ørsted, Bent (1991), "Explicit functional determinants in four dimensions", Proceedings of the American Mathematical Society 113 (3): 669–682, doi:10.2307/2048601, ISSN 0002-9939, MR1050018.
- Chang, Sun-Yung A. (1999), "A fourth order differential operator in conformal geometry", in M. Christ, C. Kenig and C. Sadorsky, Harmonic Analysis and Partial Differential Equations; Essays in honor of Alberto P. Calderon, Chicago Lectures in Mathematics, pp. 127–150.
- Paneitz, Stephen M. (2008), "A quartic conformally covariant differential operator for arbitrary pseudo-Riemannian manifolds (summary)", SIGMA. Symmetry, Integrability and Geometry. Methods and Applications 4: Paper 036, 3, doi:10.3842/SIGMA.2008.036, ISSN 1815-0659, MR2393291.